Chapter 12: Recursive Iteration, Rootfinding and Newton’s Method

Return to all notes

Rootfinding and the Bisection method

Recall that we encountered the Bisection method in Chapter 5. This was another way to do rootfinding. If we reenter the bisection procedure:

bisect := proc (f::procedure, interval::range,{eps:=10^(-4)})::numeric;
  description "This procedure performs the bisection method on the function f with given range.  The parameter eps will determine  the halting condition."
  local mid := .5*(lhs(interval)+rhs(interval));
  local inter := interval;
  if f(rhs(inter))*f(lhs(inter))>0 then
     error "A root is not guaranteed to be in this interval.":
  end if:
  while rhs(inter)-lhs(inter) > eps do
    if f(lhs(inter))*f(mid) < 0 then
      inter := lhs(inter) .. mid
    else
      inter := mid .. rhs(inter)
    end if;
    mid := .5*(lhs(inter)+rhs(inter));
  end do;
  return mid:
end proc:

We can find roots, like $\sqrt{2}$ using this instead.

bisect(x->x^2-2,1..2)

Exercise

Find the solution to $\cos x = x$ using the bisection method.

Recursive Iterations

Earlier, we have seen a few cases of iteration, in particular recursive iteration. For example, the sequence:
$$a_{n} = \frac{1}{a_{n-1}+1}$$
with $a_0=1$ generates a sequence. In Chapter 10 we found the first few terms and then found the limit of this. Recall that if we define:

a:=n->1/(1+a(n-1))
a(0):=1

then seq(a(n),n=1..10) generates the first 10 terms or
$$1,\frac{1}{2},\frac{2}{3},\frac{3}{5},\frac{5}{8},{\frac {8}{13}},{\frac {13}{21}},{\frac {21}{34}},{\frac {34}{55}},{\frac {55}{89}},{\frac {89}{144}}$$

and as we discovered above, this sequence converges to the golden mean (or golden ratio)
$$\frac{1+\sqrt{5}}{2}$$

Finding $\sqrt{a}$

Another useful iterative sequence is the following:
$$x_{n+1} = \frac{x_n^{2}+a}{2x_n}\qquad x_0=a$$

for a positive number $a$. We will show that this converges to $\sqrt{a}$. For example, if $a=2$, then

x:=n->(x(n)^{2}+2)/(2*x(n-1))
x(0):=2

(and again make sure that the $x_0$ is entered after the general formula.) If we find the first few terms of this we get:
$$\frac{3}{2},\frac{17}{12},\frac{577}{408},\frac{665857}{470832},\frac{886731088897}{627013566048},\ldots$$

and then the fraction gets quite large because $x_0$ is an integer and Maple is trying to keep everything as exact numbers (so returns a rational). If instead, we use $x(0):=2.0$, the rerun the first few terms:
$$2.0,1.500000000,1.416666666,1.414215686,1.414213562,
\ldots$$

Exercise.

Use the above to find $\sqrt{5}$.

Newton’s Method

(First, before trying any of these, you’ll probably want to unassign('x') to get everything to work correctly.)

The above formula is a specific case of Newton’s method for finding roots. Here’s a geometric view of Newton’s method.

We intend to find the point $x^{\star}$ such that $f(x)=0$. We don’t know how to find $x^{\star}$, but have an approximate solution, call it $x_0$. Draw the tangent line to the curve $y=f(x)$ at $x_0$. The following plot is an example with $f(x)=x^{2}-2$ and $x_0=0.4$:

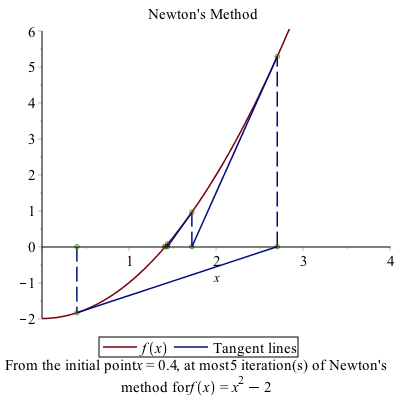
The point on the left is $x_0=0.4$ and the blue line is the tangent line there. Instead of using the function, we use the tangent line, which is easy to solve. That value is $x_1=2.7$. At this point (no pun intended), we find the tangent line at $x_1$ and find where it crosses the $x$-axis.

This process continues indefinitely and (for this example), it converges to $\sqrt{2}$.

Why this works

Recall that the tangent line to the curve $y=f(x)$ at $x=a$ is
$$y=f'(a)(x-a)+f(a)$$
and if we set $y=0$ in the tangent line because we are seeking the root (where the function is 0)
$$0=f'(a)(x-a)+f(a)$$
and then we solve for $x$. (Either by hand or let Maple do it).
$$x=a+\frac{f(a)}{f'(a)}$$

Next, if we let $a=x_0$, our initial point and $x$ be $x_1$, the next point:
$$x_1=x_0+\frac{f(x_0)}{f'(x_0)}$$

or in general:
$$x_{n+1}=x_n+\frac{f(x_n)}{f'(x_n)}$$

and this last equation is called Newton’s rootfinding method (or just Newton’s method)

Example

Use Newton’s method to find the solution to $\cos x = x$.

If we let $f(x)=x-\cos x$ and perform Newton’s method. Since, $f'(x)=1+\sin x$, this means that
$$x_{n+1} = x_n - \frac{x_n-\cos x_n}{1+\sin x_n}$$
and let’s use $x_0=0$ as an initial guess.

In Maple, if we enter:

x:=n->x(n-1)-(x(n-1)-cos(x(n-1)))/(1+sin(x(n-1)))
x(0):=0.0

and then seq(x(n),n=0..5) results in
$$0., 1.000000000, 0.7503638679, 0.7391128909, 0.7390851334, 0.7390851332$$

As you can see from the sequence, the last two numbers are the same for the first 9 digits.

And looking at a plot of $x$ and $\cos x$,

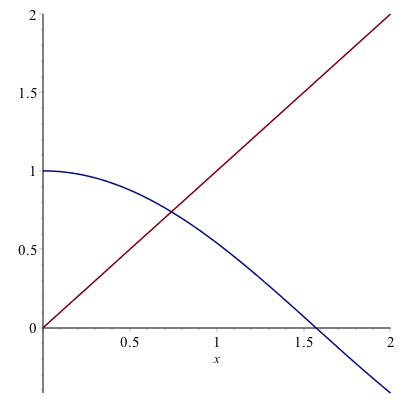
The solution looks like about 0.73.

Exercise

There are two $x$ values such that $1-x^{2}=\sin x$. Find the solution that satisfies $x\lt 0$. Plot the two function to see if your answer is reasonable.

Using the built-in NewtonsMethod command

There is a command called NewtonsMethod in the Student[Calculus1] package. Look at the Help Browser for the command and explore the options. Reproduce the problems above.